[ Übersicht
]
[ Installation
]
[ Namenskonvention
]
[ In/Output
]
[ Parameterfile
]
[ Demos
]
[ to do
]
[ A. Röttig
]
J. Menz:
Demonstrationen zur Wirkungsweise der Stellgrößen und der Meßstellenanordnung bei geostatistischen Vorhersagen
An der Instruktion haben mitgearbeitet:
Dr.-Ing. N. Kolesnikov: bei der Berechnung der Anschauungsbeispiele
Dr.-Ing. A.
Röttig: bei der Bereitstellung der Software, der notwendigen
Parameterfiles
für die Berechnung der Demos und der WEB-Präsentation
- Einführung
- Demonstrationsbeispiele zum Ordinary Kriging bei unzureichendem Erkundungsgrad
- Demonstrationsbeispiele zum gewöhnlichen Gradienten-Kriging bei ausreichendem Erkundungsgrad
- Demonstrationen zum Ordinary Kriging bei ausreichendem Erdkundungsgrad
- Demonstrationen zum Universal Kriging
- Demonstrationen zum universellen Gradienten-Kriging
- Demonstrationen zum Co- und Gradienten-Kriging und das Prinzip der vollständigen Erfassung
- Demonstrationen zum gewöhnlichen und universellen Co-Kriging beim Auftreten eines Trends
- Demonstrationen zum BAYESschen Kriging
- Vergleich mit BEZIER-Kurven
- Vorhersagen mit der Multiquadratischen Methode auf der Basis von Stützwerten
- Kernfunktionsbasierte Vorhersagen mit Gradienten
- Zum Einfluß des Meßstellenabstandes auf die Vorhersagen
Im folgenden soll an Anschauungsbeispielen gezeigt werden, wie man durch die Wahl der Stellgrößen
- Modellparameter,
- Trendannahmen,
- Meßdatenauswahl
und durch die Meßstellenanordnung die Vorhersageergebnisse beeinflussen kann. Mit dieser Zusammenstellung von Anschauungsbeispielen soll die Einarbeitung in die Geostatistik und in die Nutzung unserer Software erleichtert werden. Die Anschauungsbeispiele sollen zu einer effektiven Anwendung der entwickelten Software beitragen.
Zur Demonstration der Effekte, die sich durch die Wahl der Stellgrößen und Meßstellenanordnung erzielen lassen, sind Profildarstellungen besonders geeignet. Deshalb werden die Demonstrationen an Profildarstellungen durchgeführt. Gezeigt werden soll, wie man über die Vorhersage an Punkten - d.h. durch Punktkriging - den Verlauf der Gebirgs- und Lagerstättenparameter prognostizieren kann. Die Vorhersage von Durchschnittswerten in vorgegebenen Raumbereichen durch Blockkriging ist Gegenstand eines weiteren Forschungsberichtes, der der Volumen- und Vorratsberechnung gewidmet ist. Sie wird hier nicht betrachtet.
In den folgenden Abschnitten sollen Vorhersagen diskutiert werden, die sich als Sonderfälle des BAYESschen universellen Co- und Gradienten-Krigings mit Filterung von Störgrößen ableiten lassen [MENZ (1994a), MENZ/PILZ (1994), MENZ (1996a)]. Begonnen wird mit Ordinary Kriging, der einfachsten geostatistischen Vorhersage auf der Grundlage von Stützwerten.
Bei den nun folgenden Anschauungsbeispielen handelt es sich um Vertikalschnitte durch das Gebirge. In der Schnittebene wird die Spur einer Fläche gezeigt, die z. B. zwei unmittelbar benachbarte geologische Schichten voneinander abgrenzen könnte. Die dünn ausgezogene Linie soll den tatsächlich in der Natur ausgebildeten Verlauf dieser Fläche im Profil widerspiegeln und somit die Sollwerte für die Höhen der Trennfläche vorgeben, aus denen man einerseits die Meßwerte und Gradienten entnehmen kann, die als Erkundungsdaten angesehen werden sollen. Andererseits dienen diese Sollwerte zum Vergleich der Modellierungsergebnisse, die auf der Grundlage der geostatistischen Vorhersagen aus den entnommenen Meßwerten und Gradienten abgeleitet werden können. Die Stellen, an denen Meßwerte entnommen worden sind, werden durch Punkte markiert. Die Entnahme von Gradienten wird durch Pfeile angegeben.
Der Modellverlauf wird durch eine stark ausgezogene Linie in den Demos dargestellt. Durch eine etwas dünnere unterbrochene Linie wird in den Anschauungsbeispielen der Trend angegeben, der sich beim Ordinary Kriging auf den Mittelwert reduziert. Alle Zahlenangaben, die sich auf Längen beziehen, erfolgen in Metern. Die Dimension wird bei der Angabe der Modellparameter und Einwirkungsbereiche in den Demos meist weggelassen.
Die zu modellierende Fläche ist eine Fläche topographischer Ordnung. Will man den Verlauf einer solchen Fläche durch Höhenmessung optimal erfassen, dann muß man auf den Kamm- und Tallinien messen. Im Profil hat man die Höhen der Extrema zu bestimmen. Bei der Erfassung durch Gradienten wäre dagegen der Anstieg des Profils an den Wendepunkten zu messen.
Alle Demos, die in diesem Forschungsbericht behandelt werden, befinden sich in Anlage 1. Bei der Charakterisierung der Demos in Anlage 1 werden bestimmte Begriffe benutzt, die an dieser Stelle nochmals erklärt werden sollen. Von globaler Vorhersage wird gesprochen, wenn alle Messungen in die Vorhersage einbezogen werden. Von lokaler Vorhersage spricht man, wenn bei der Vorhersage nur auf die Messungen aus einem Einwirkungsbereich EWB zurückgegriffen wird. Die Vorhersage heißt angepaßt, wenn der Range, ein Maß für die Reichweite der Nachbarschaftsbeeinflussung, auf die Daten abgestimmt worden ist.
In den Demos 1 bis 10 geht man davon aus, daß aus der geologischen Erkundung lediglich vier Stützwerte vorliegen, die die in den Demos markierten Stützpunkte festlegen und auf deren Basis das vorgegebene Profil bei der Vorhersage nur unvollständig erfaßt werden kann, was auch die Modellierung zeigt. Nach BUKRINSKIJ sind die hier benutzten Erkundungsdaten nicht "ergodisch", weil durch sie nicht alle wesentlichen Extrema erfaßt worden sind [MENZ (1991 b)]. Trotzdem eignet sich gerade dieser Datensatz gut, um bestimmte Effekte deutlich zu machen.
Zum Beispiel haben geostatistische Vorhersagen die Eigenschaft, sich in Bereichen guter Nachbarschaftsbeeinflussung der einfachen linearen Interpolation zu nähern. Das tritt ein, wenn 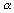 , die Dämpfung der Autokorrelation, klein, also der Range groß ist und die Meßstellen dicht beieinander liegen. Im Falle abnehmender Nachbarschaftsbeeinflussung nähert sich die geostatistische Vorhersage dem Trend bzw. Mittelwert. Die Nachbarschaftsbeeinflussung, der Range, nimmt ab, wenn
, die Dämpfung der Autokorrelation, klein, also der Range groß ist und die Meßstellen dicht beieinander liegen. Im Falle abnehmender Nachbarschaftsbeeinflussung nähert sich die geostatistische Vorhersage dem Trend bzw. Mittelwert. Die Nachbarschaftsbeeinflussung, der Range, nimmt ab, wenn 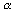 und die Abstände zwischen den Meßstellen zunehmen. Bei fehlender Autokorrelation deckt sich die Vorhersage mit dem Trend. Genau dieses sinnvolle und erwünschte Verhalten geostatistischer Vorhersagen zeigen die Demos 1 bis 10.
In den Demos 1 und 2 wird für eine GAUSSsche Kovarianzfunktion (q=2) demonstriert, wie sich die Änderung von
und die Abstände zwischen den Meßstellen zunehmen. Bei fehlender Autokorrelation deckt sich die Vorhersage mit dem Trend. Genau dieses sinnvolle und erwünschte Verhalten geostatistischer Vorhersagen zeigen die Demos 1 bis 10.
In den Demos 1 und 2 wird für eine GAUSSsche Kovarianzfunktion (q=2) demonstriert, wie sich die Änderung von 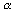 auswirkt. Die Demos 3 und 4 zeigen das gleiche für die exponentielle Kovarianzfunktion (q=1). Wie sich die Vorhersage dem Mittelwert bei fehlender Nachbarschaftsbeeinflussung nähert, ist in den Demos 1, 3, 5, 7 und 9 sehr deutlich zu sehen. Beim Vergleich der Demos 1 und 2 mit den Demos 3 und 4 fällt außerdem auf, daß die exponentielle Kovarianzfunktion zu spitz zulaufenden Bergen und Tälern führt, während die GAUSSsche Kovarianzfunktion abgerundete Erhebungen und Senken erzeugt und darüber hinaus zu deutlichen Überhöhungen führen kann, wenn eine starke Nachbarschaftsbeeinflussung vorliegt (Demo 2). Solche Überhöhungen treten bei exponentiellen Kovarianzfunktionen nicht auf.
Das Glättungsverhalten geostatistischer Vorhersagen läßt sich gut an einem Vergleich mit der geostatistischen Simulation erklären. Vergleicht man meßpunkttreue geostatistische Vorhersagen mit ebenfalls meßpunkttreuen bedingten geostatistischen Simulationen, dann stellt man fest, daß man sich im Mittel über eine zunehmende Zahl von Simulationen dem durch Kriging vorhergesagten Verlauf nähert. Eine durch bedingte geostatistische Simulation erzeugte Realisierung soll hinsichtlich der Variabilität ein ähnliches Erscheinungsbild wie die in der Natur ausgebildete Realisierung zeigen. Aus diesem Grund benutzt man zum Beispiel die geostatistische Simulation, wenn zu prüfen ist, wie eine geplante neue Technologie mit der natürlichen Veränderlichkeit der Gebirgs- und Lagerstättenparameter zurechtkommt.
Kriging dagegen führt zu einem geglätteten Verlauf der Gebirgs- und Lagerstättenparameter zwischen den Stützpunkten, der das Wesentliche, Generelle zeigt. Solche Vorhersagen werden für die Bearbeitung vieler Aufgaben gebraucht. Es gibt aber auch Aufgaben, bei denen das Glättungsverhalten stört und deshalb kompensiert werden muß. Ausgereifte Verfahren zur Glättungskompensation des Krigings gibt es noch nicht, wohl aber Vorschläge, auf die in der Literatur und in der noch folgenden Fallstudie "Drehwaagegeoid" eingegangen wird [OLEA/PAWLOWSKY (1996), MENZ (1997 c)].
In diesem Abschnitt soll nur auf das unterschiedliche Glättungsverhalten von exponentiellen und GAUSSschen Kovarianzfunktionen am Beispiel der Demos 1 und 3 sowie 2 und 4 hingewiesen werden. Beim exponentiellen Modell q = 1 ist der Glättungseffekt deutlicher ausgeprägt. Er nimmt mit dem Anstieg von a
zu. Dagegen führt ein zu kleines a
, also ein zu großer Range, insbesondere im GAUSSschen Fall q = 2 zu einer Überschwingung, wie Demo 2 zeigt. Eine GAUSSsche Kovarianzfunktion ist beliebig oft differenzierbar. Sie liefert ausgerundete fließende Übergänge in den Vorhersagen.
Eine besondere Eigenschaft ist, daß sich geostatistische Vorhersagen bei fehlender Nachbarschaftsbeeinflussung dem Trend anpassen. Deshalb soll bereits an diesen Demos 1 bis 10 darauf aufmerksam gemacht werden, daß sich für die optimale Schätzung des Trends aus den Meßwerten unterschiedliche Werte ergeben, wenn sich die Kovarianzfunktion hinsichtlich des Typs (hier q = 1 oder 2) und hinsichtlich der Parameter (hier a
und c) ändert. Beim Ordinary Kriging (OK) gilt für den Trend
auswirkt. Die Demos 3 und 4 zeigen das gleiche für die exponentielle Kovarianzfunktion (q=1). Wie sich die Vorhersage dem Mittelwert bei fehlender Nachbarschaftsbeeinflussung nähert, ist in den Demos 1, 3, 5, 7 und 9 sehr deutlich zu sehen. Beim Vergleich der Demos 1 und 2 mit den Demos 3 und 4 fällt außerdem auf, daß die exponentielle Kovarianzfunktion zu spitz zulaufenden Bergen und Tälern führt, während die GAUSSsche Kovarianzfunktion abgerundete Erhebungen und Senken erzeugt und darüber hinaus zu deutlichen Überhöhungen führen kann, wenn eine starke Nachbarschaftsbeeinflussung vorliegt (Demo 2). Solche Überhöhungen treten bei exponentiellen Kovarianzfunktionen nicht auf.
Das Glättungsverhalten geostatistischer Vorhersagen läßt sich gut an einem Vergleich mit der geostatistischen Simulation erklären. Vergleicht man meßpunkttreue geostatistische Vorhersagen mit ebenfalls meßpunkttreuen bedingten geostatistischen Simulationen, dann stellt man fest, daß man sich im Mittel über eine zunehmende Zahl von Simulationen dem durch Kriging vorhergesagten Verlauf nähert. Eine durch bedingte geostatistische Simulation erzeugte Realisierung soll hinsichtlich der Variabilität ein ähnliches Erscheinungsbild wie die in der Natur ausgebildete Realisierung zeigen. Aus diesem Grund benutzt man zum Beispiel die geostatistische Simulation, wenn zu prüfen ist, wie eine geplante neue Technologie mit der natürlichen Veränderlichkeit der Gebirgs- und Lagerstättenparameter zurechtkommt.
Kriging dagegen führt zu einem geglätteten Verlauf der Gebirgs- und Lagerstättenparameter zwischen den Stützpunkten, der das Wesentliche, Generelle zeigt. Solche Vorhersagen werden für die Bearbeitung vieler Aufgaben gebraucht. Es gibt aber auch Aufgaben, bei denen das Glättungsverhalten stört und deshalb kompensiert werden muß. Ausgereifte Verfahren zur Glättungskompensation des Krigings gibt es noch nicht, wohl aber Vorschläge, auf die in der Literatur und in der noch folgenden Fallstudie "Drehwaagegeoid" eingegangen wird [OLEA/PAWLOWSKY (1996), MENZ (1997 c)].
In diesem Abschnitt soll nur auf das unterschiedliche Glättungsverhalten von exponentiellen und GAUSSschen Kovarianzfunktionen am Beispiel der Demos 1 und 3 sowie 2 und 4 hingewiesen werden. Beim exponentiellen Modell q = 1 ist der Glättungseffekt deutlicher ausgeprägt. Er nimmt mit dem Anstieg von a
zu. Dagegen führt ein zu kleines a
, also ein zu großer Range, insbesondere im GAUSSschen Fall q = 2 zu einer Überschwingung, wie Demo 2 zeigt. Eine GAUSSsche Kovarianzfunktion ist beliebig oft differenzierbar. Sie liefert ausgerundete fließende Übergänge in den Vorhersagen.
Eine besondere Eigenschaft ist, daß sich geostatistische Vorhersagen bei fehlender Nachbarschaftsbeeinflussung dem Trend anpassen. Deshalb soll bereits an diesen Demos 1 bis 10 darauf aufmerksam gemacht werden, daß sich für die optimale Schätzung des Trends aus den Meßwerten unterschiedliche Werte ergeben, wenn sich die Kovarianzfunktion hinsichtlich des Typs (hier q = 1 oder 2) und hinsichtlich der Parameter (hier a
und c) ändert. Beim Ordinary Kriging (OK) gilt für den Trend
 ( 4.1 )
( 4.1 )
OK kann als Sonderfall des Universal Kriging (UK) angesehen werden, bei dem mit einem Trendpolynom nullter Ordnung
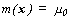 ( 4.2 )
( 4.2 )
gearbeitet wird. Der in den Demos 1 bis 10 eingezeichnete Mittelwert wurde unter Annahme dieses Sonderfalls (4.2) geschätzt. Die Äquivalenz zwischen UK und Kollokation [MENZ/PILZ (1994)] nutzend, wird m
0 über eine Schätzung nach der verallgemeinerten Methode der kleinsten Quadrate (MKQ) in unserem Softwaremodul Kollokation bestimmt. In [WACKERNAGEL (1995)] findet man für die Lösung dieser Aufgabe in Kapitel 10 "Kriging the Mean" eine Extraableitung.
Diese Ausführungen zum Trend bzw. Mittelwert bei autokorrelierten Messungen sind wichtig, damit der Nutzer der Software nicht mit dem einfachen arithmetischen Mittel aus den 4 Stützpunkten in den Demos 1 bis 10 vergleicht. Obwohl beim OK modellgemäß der Trend konstant ist, läßt sich doch eine flexible Trendberücksichtigung vornehmen, wenn man nur mit den Meßwerten aus einem Einwirkungsbereich arbeitet (lokales Kriging).
In den Demos 5 und 7 - 10 wird gezeigt, daß beim Auftreten von Störgrößen R, d. h. im Falle
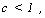 ( 4.3 )
( 4.3 )
eine Filterung erfolgt. Die Extrema werden beschnitten. Die Meßpunkttreue wird verlassen. Es tritt eine zusätzliche Glättung ein, was in den Demos 5 und 6 deutlich zu sehen ist, wo wegen c = 0,75 die Streuung der Störgröße 25 % der Gesamtstreuung ausmacht. In der Demo 6 wird gezeigt, wie die Modellierung aussehen würde, wenn man beim Auftreten von Störgrößen die Meßpunkttreue erzwingt, was aber unsinnig ist. Dieser unsinnige Fall tritt ein, wenn man die Elemente der Kovarianzmatrix und des Kovarianzvektors im Falle (4.3) nach der gleichen Vorschrift berechnet. Demo 8 ist mit Demo 2 vergleichbar. Trotz Störgröße tritt in Demo 8 ein Überschwingen auf. In den Demos 7 bis 10 ist die Störgrößenstreuung konstant. Die Unterschiede resultieren dort aus den Unterschieden in a
und q.
Nun soll gezeigt werden, daß sich die innere Geometrie einer Fläche, die in einer vertikalen Schnittebene betrachtet wird, über Gradienten vollständig erfassen läßt. Zu diesem Zweck sind an den insgesamt 10 Wendepunkten des betrachteten Profilauschnittes Gradienten bestimmt und für die Vorhersage durch Gradienten-Kriging bereitgestellt worden. Mit einem Stützwert zur absoluten Orientierung ist diese Datenmenge gerade ausreichend für die vollständige Vorhersage des Profilverlaufes im betrachteten Ausschnitt, was in den weiteren Ausführungen gezeigt werden soll. Zunächst wird davon ausgegangen, daß wieder so ein Modell wie beim Ordinary Kriging vorliegt, bei dem sich der Trend auf den Sonderfall, konstanter Erwartungswert, reduziert. Deshalb wird in der Überschrift auch von gewöhnlichem Gradienten-Kriging gesprochen, das in den nun folgenden Demos 11 bis 20 betrachtet werden soll.
In die Schätzung des Mittelwertes, die wieder über die verallgemeinerte MKQ unter Benutzung der Module für die Kollokation im Sonderfall (4.2) erfolgt, gehen dieses Mal auch die Gradienten ein. Welchen starken Einfluß sie nehmen, erkennt man in den Demos 19 und 20, bei denen nur ein Stützwert verwendet wird, und zwar in Demo 19 an der Stelle eines Maximums und in Demo 20 an der Stelle eines Minimums.
In den Demos 11 bis 16 wird am Beispiel von 10 Gradienten und 1 Stützwert gezeigt, wie sich eine Variation des Range, der Reichweite der Nachbarschaftsbeeinflussung, die über die Änderung von a
realisiert wird, auf die Vorhersagen auswirkt. Der Wert von a
= 0,01 m-1 in Demo 14 wird als geeignet angesehen und in den weiteren Demos benutzt, die mit dem Attribut "angepaßt" bezeichnet worden sind. Ein zu großer Range erhöht die Schwingungsamplituden und führt zu größeren Wellenlängen (Demo 11). Ein zu kleiner Range hat die entgegengesetzte Wirkung (Demo 16).
Vergleicht man nun alle Demos, die mit dem abgestimmten Range (a
= 0,01 m-1) modelliert worden sind (Demos 14, 19, 20), dann sieht man, daß die Anordnung des einen Stützwertes, der die Integrationskonstante beim gewöhnlichen Gradienten-Kriging festlegt, keinen wesentlichen Einfluß hat und daß auch die Verwendung von 2 Stützwerten in den Demos 17 und 18 keine wesentliche Verbesserung der Modellierungsergebnisse bringt. Letzteres liegt daran, daß alle weiteren Messungen, die diesem Datensatz hinzugefügt werden, keine neuen Informationen enthalten. Sie sind redundant.
In den Demos 21 bis 24 wird ein Erkundungsdatensatz benutzt, der die Stützwerte sämtlicher Extremstellen umfaßt und damit die vollständige Information für die Vorhersage des Profils enthält. In Demo 21 sieht man, wie gut die Vorhersage mit den Sollwerten übereinstimmt, wenn mit der angepaßten Kovaranzfunktion gearbeitet wird (a
= 0,01 m-1, q = 2).
Bekanntlich treten bei Verwendung einer GAUSSschen Kovarianzfunktion numerische Probleme auf, so daß die Invertierung der Kovarianzmatrix oft erst nach Einführung einer Regularisierungskonstante (von etwa 1 %) gelingt. In Demo 22 kann gezeigt werden, daß eine Regularisierungskonstante von 1 % (c = 0,99) das Vorhersageergebnis von Demo 21 (ohne Regularisierungskonstante) fast nicht verändert, so daß man dieses Hilfsmittel eigentlich ohne nachträgliche Kompensation benutzen darf.
In den Demos 23 und 24 wurde der Abstand zwischen dem 7. und 8. Stützwert bewußt weiter auseinandergezogen, um an diesem veränderten Datensatz demonstrieren zu können, welche Effekte zu erwarten sind, wenn nur die Werte aus einem relativ begrenzten Einwirkungsbereich zur Vorhersage herangezogen werden (lokales Kriging mit EWB = 350 m). Im Unterschied zu globalem Kriging tritt in Demo 24 beim lokalen Kriging mit gleicher Kovarianzfunktion ein kantiger Profilverlauf zwischen den Meßpunkten 7 und 8 auf. Er kommt dadurch zustande, daß der EWB wandert und die Meßpunktauswahl ändert, was zu Knicken und Sprüngen führt. Dagegen werden beim globalen Kriging stets alle Meßwerte berücksichtigt, so daß bei q = 2 glatte Profilverläufe erzeugt werden. In Demo 23 ist lokales Kriging mit einer exponentiellen Kovarianzfunktionen (a
= 0,01 m-1, q = 1) zu sehen. Man erkennt wieder die Sprünge im Verlauf zwischen den Meßpunkten 7 und 8 und außerdem, daß das exponentielle Modell für die Vorhersage des vorgegebenen Sollprofils ungünstiger ist als das GAUSSsche.
Beim Universal Kriging (UK) wird der Trend berücksichtigt. In unserer Software ist als Trendfunktion ein Polynom bis zur Ordnung 3 zugelassen. Zur Demonstration des UK wird dem Sollprofil ein linearer Trend überlagert, der im Ursprung beginnt und dessen Anstieg 10 % beträgt (siehe Trend (Soll) in Demo 32). Das so erzeugte geneigte Sollprofil ist Grundlage weiterer Demos. In Demo 25 und 28 werden nur 4 Stützwerte benutzt, die dem geneigten Sollprofil entnommen worden sind. Der Erkundungsgrad ist unzureichend. In Demo 26 ist dagegen die Vorhersage zu sehen, die aus den Stützwerten aller 11 Extrema abgeleitet worden ist.
In den Demos 25, 27 und 28 soll gezeigt werden, daß die Vorhersagen auch beim UK im Falle fehlender Nachbarschaftsbeeinflussung mit dem Trend zusammenfallen. Der Trend wird, wie bereits gesagt, aus den zur Verfügung stehenden Erkundungsdaten über eine verallgemeinerte MKQ-Schätzung bestimmt, und zwar mit dem Modul Kollokation. In den Demos 25 bis 29 wurden stets die gleichen Modellparameter benutzt, so daß die Unterschiede im Trend nur aus den Unterschieden in den bereitgestellten Stützwerten resultieren. In Demo 25 und 28 sind es jeweils 4 und in Demo 26 und 27 jeweils 11 unterschiedlich angeordnete Stützwerte. In den Demos 29, 30 und 31 ist der Trend immer aus 100 Stützwerten jedoch mit variablem Range (a
= 0,01 ; 0,075 und 0,005 m -1) bestimmt worden. In Demo 32 werden schließlich unterschiedliche Trendverläufe zum Vergleich in einer Zeichnung dargestellt. An Demo 26 sollte gezeigt werden, daß UK bei angepaßter Kovarianzfunktion sehr gute Vorhersagen liefert. Schließlich sei erwähnt, daß bei allen Demos zum UK globales Kriging benutzt worden ist.
Im folgenden soll gezeigt werden, daß beim Gradienten-Kriging auch Trends berücksichtigt werden können. Das für diesen Fall konzipierte und in SAFARI implementierte Verfahren soll als universelles Gradienten-Kriging bezeichnet werden. Ausgegangen wird nun wie im vorhergehenden Abschnitt von einem linear ansteigenden Sollprofil, von dem die Gradienten, die an allen 10 Wendepunkten ermittelt worden sind, für die Vorhersage bereitgestellt werden. Mit einem Stützwert für die absolute Orientierung, ist dieser Datensatz ausreichend für die vollständige Modellierung, wie in den Demos 33 und 34 gezeigt wird. Daß ein zweiter Stützwert auch hier keine neue Information bringt, zeigen die Demos 35 und 36. In allen Demos wurde globales Kriging mit einer angepaßten Kovarianzfunktion (a
= 0,01 m-1, q = 2) durchgeführt. In den Demos 33 bis 36 wird gezeigt, daß die Lage der Stützpunkte keine Rolle spielt, wenn der Profilverlauf vollständig durch Gradienten erfaßt worden ist. In den Demos 35 und 36 wird der Schwerpunkt der Stützwerte durch ein Quadrat angegeben, der aus dem einfachen arithmetischen Mittel bestimmt worden ist. Seine Lage hat keinen Einfluß auf die Vorhersage und auf den Trend, der wieder aus einer verallgemeinerten MKQ Schätzung abgeleitet wird, und zwar dieses Mal für ein Polynom 1. Ordnung unter Berücksichtigung der Gradienten. Die Lösung dieser Aufgabe liefert wieder der Modul für die Kollokation.
Das in [MENZ (1994 b) (1995)] beschriebene sogenannte Prinzip der vollständigen Erfassung sagt aus, daß nur dann durch Co-Kriging gute Vorhersagen zu erwarten sind, wenn der wesentliche Verlauf der Co-Variablen durch Stützwerte erfaßt worden ist und außerdem die Einwirkungsbereiche bei der Vorhersage so gewählt werden, daß der Verlauf der Co-Variablen bis zu den Stützstellen des zu modellierenden Merkmals verfolgt werden kann, also nicht durch einen zu gering gewählten Einwirkungsbereich der Co-Varibalen unterbrochen wird. Prinzipiell sind diese Aussagen auf Gradienten-Kriging übertragbar, wenn man die partiellen Ableitungen des Merkmals Z nach den Koordinaten x, y, ... als Co-Variablen ansieht.
In den nun folgenden Demos soll für Co- und Gradienten-Kriging gezeigt werden, zu welchen Auswirkungen eine Verletzung des Prinzips der vollständigen Erfassung führen kann. In Demo 37 wird zunächst durch gewöhnliches Gradienten-Kriging mit einer angepaßten Kovarianzfunktion und einem für die vollständige Beschreibung ausreichendem Satz von Gradienten vorhergesagt. Die Einwirkungsbereiche für Stützwerte EWBs und Gradienten EWBg wurden mit 1100 m so groß gewählt, daß alle Messungen berücksichtigt werden (im Prinzip globales Kriging). Der mit den an den Rändern angeordneten Stützpunkten vorhergesagte Profilverlauf von Demo 37 soll nun mit dem in Demo 38 verglichen werden, bei dem das Prinzip der vollständigen Erfassung durch den zu klein gewählten Einwirkungsbereich für Gradienten verletzt worden ist.
In den Demos 39 und 40 wird der gleiche Effekt für eine Co-Variable H gezeigt, die genau so wie das Sollprofil, nur um 25 m höhenversetzt, verläuft. Sie könnte die an allen Extremstelle durch Stützwerte erkundete Hangendbegrenzung eines Flözes sein, während das zu modellierende Merkmal, beispielsweise das Flözliegende L, lediglich durch 2 Stützwerte erfaßt worden ist. Die Kreuzkovarianzfunktion zwischen H und L soll auf Grund der vorausgesetzten Ähnlichkeit von H und L der Autokorrelationsfunktion von L bzw. H entsprechen. Unter dieser Annahme wird Co-Kriging mit den Parametern q = 2, c = 1 und a
= 0,01 m-1 durchgeführt. In Demo 39 werden die Einwirkungsbereiche für H und L ausreichend groß gewählt (globales Kriging). Man sieht, wie gut sich mit Co-Kriging vorhersagen läßt.
In Demo 40 wird dagegen das Prinzip der vollständigen Erfassung verletzt, weil für H mit EWBH = 350 m ein zu geringer Einwirkungsbereich gewählt worden ist. Für L wurde EWBL = 1100 m beibehalten. In den Demos 41 und 42 wird der gleiche Effekt nochmals für eine um phi = 50 m phasenversetzte Co-Variable gezeigt. An Demo 41 ist zu sehen, wie gut über Co-Kriging auch beim Vorliegen einer Phasenverschiebung vorhergesagt werden kann und an Demo 42, welche Abweichungen auftreten, wenn in diesem Fall das Prinzip der vollständigen Erfassung verletzt wird.
In den folgenden Demos wird den Sollkurven für die Co-Variable und für das Merkmal der gleiche lineare Trend (Anstieg 5 %) aufgeprägt, um zeigen zu können, wie Co-Kriging bei trendbehafteten Meßwerten funktioniert. Wieder werden von der Co-Variablen Stützwerte an allen 11 Extremstellen entnommen und für das zu modellierende Merkmal lediglich zwei Stützwerte vorgegeben. In Demo 43 wird gewöhnliches Co-Kriging mit den gleichen Modellparameter wie in Demo 41 auf diese Daten angewandt. Man sieht, daß brauchbare Ergebnisse erzielt werden können. An Demo 44 wird gezeigt, wie dagegen universelles Co-Kriging arbeitet. In diesem Fall wurde sowohl für die Co-Variable als auch für das Merkmal in den Ansatz ein Trendpolynom 1. Ordnung aufgenommen und mit den gleichen Modellparametern wie in Demo 43 vorhergesagt. Das Ergebnis der Vorhersage kann mit Dem 43 verglichen werden. Es entspricht den Sollwerten noch besser. In Demo 44 ist außerdem der nach der verallgemeinerten MKQ (hier über den Modul Kollokation ) geschätzte Trend des Merkmals angegeben. In diese Schätzung gehen die Stützwerte der Co-Variablen ein.
Mit Demonstrationen zum BAYESschen Kriging sollen die Beispiele zur geostatistischen Vohersage abgeschlossen werden. Ausgehend von den Sollwerten für die Co-Variable und für das Merkmal, die den Demos 43 und 44 zugrunde gelegt worden sind, soll nun mit den gleichen Datensätzen und Modellparametern demonstriert werden, wie BAYESsches Kriging arbeitet. Ein anschauliches Beispiel erhält man, wenn beispielsweise, wie in Demo 49 gezeigt, Daten der Co-Variablen wieder vom Trend befreit werden. Sie können, wie eben angegeben, durch Co-Kriging berücksichtigt werden. Der Trend dagegen wird als a priori-Kenntnis angesehen und soll über m
o und T0 im BAYESschen Sinne in die Vorhersage eingehen. Mit zwei Stützwerten für das Merkmal erhält man über BAYESsches Co-Kriging im vorliegenden Fall das in Demo 50 vorgestellte Vorhersageergebnis. Vergleicht man es mit Co-Kriging in Demo 44, dann stellt man eine noch bessere Anpassung an das Sollprofil fest. In Demo 50 werden die zusätzlichen Informationen (Trend und Co-Variable) mit dargestellt.
Am Beispiel der Demos 45 bis 48 soll dagegen gezeigt werden, daß bei ungünstiger Nutzung der Möglichkeiten des BAYESschen Krigings auch ungünstige Vorhersagen zustande kommen. Angenommen wird nun, daß Vorkenntnisse zum quadratischen Trend die Vorhersage des Merkmals im BAYESschen Sinne verbessern können, die aus einem zweiten, aus einer früheren Erkundungsphase vorliegenden Datensatz abgeleitet werden können. Dieser Datensatz entspricht den Stützwerten der Co-Variablen aus Demo 39. An den Demos 45 und 46 wird gezeigt, welchen unterschiedlichen Verlauf die Vorkenntnisse zum Trend annehmen, wenn sie wie in Demo 45 über ein gleitendes Mittel aus jeweils 3 Stützwerten bestimmt werden oder wie in Demo 45 aus jeweils allen 11 Stützwerten. Im letzten Fall eigenen sie sich nicht für eine BAYES-Verbesserung der Vorhersage. Deshalb werden in den Demos 47 und 48 nun die BAYESschen Vorkenntnisse aus Demo 45 benutzt. In der Tabelle unter Demo 45 wird gezeigt, wie diese Vorkenntnisse beispielsweise für die Vorhersage an der Stelle s = 500 m aussehen können. Angegeben worden sind die Werte von m
o und T0 . In Demo 47 wird nun gezeigt, wie die BAYESsche Vorhersage aussieht, wenn diese Vorkenntnisse aus Demo 45 benutzt werden und stets mit allen 4 Stützwerten des Merkmals vorhergesagt wird. Im Unterschied dazu wird in Demo 48 stets nur der unmittelbar benachbarte Stützwert des Merkmals zusammen mit den Vorkenntnissen aus Demo 45 zur Vorhersage herangezogen. Beide Versuche sind unbefriedigend. In den Demos 47 und 48 sind die Stützwerte mit (alt) und (neu) markiert worden, wobei diese Attribute eine ältere und eine neue Messung bezeichnen sollen. Die ältere Messung bildete die Grundlage für die Angabe der Vorkenntnisse m
o und T0.
An den Beispielen erkennt man, daß plausible Vorhersagen auch unter Benutzung unterschiedlicher Verfahren bereitgestellt werden können. So war es zum Beispiel möglich, über gewöhnliches und universelles Co-Kriging zum gleichen Ergebnis wie über BAYESsches Co-Kriging zu kommen (Demo 43, 44 und 45). Schon gewöhnliches Gradienten-Kriging könnte ähnliche Vorhersagen wie universelles Gradienten-Kriging in den Demos 33 - 36 liefern. Gravierende Unterschiede ergeben sich dann allerdings bei der Vorhersage des Trends, die aus der angenommenen unterschiedlichen Ordnung im Polynomansatz resultieren. Ein ähnliches Verhalten liegt z. B. vor, wenn in Demo 26 mit Ordinary Kriging vorhergesagt wird.
In Zeichenprogrammen, wie z. B. Corel DRAW, Word-Perfect-Präsentation u. a., hat man die Möglichkeit, unregelmäßige Kurvenverläufe unter Nutzung des Moduls BEZIER zu gestalten. Als Informationen gehen ein: Stützpunkte, die links- und rechtsseitigen Tangenten sowie die links- und rechtsseitigen Krümmungsradien. Auf Grund dieser Informationen ist man in der Lage, gewünschte Kurvenverläufe zu konstruieren, und zwar leicht, weil es die Software erlaubt, eingegebene Informationen anschließend zu bearbeiten, d. h. sie zu verändern, sie zu ergänzen und sie zu löschen.
In Demo 51 wird nun gezeigt, wie das vorgegebene Sollprofil unter Nutzung dieser Möglichkeiten durch eine BEZIER-Kurve approximiert werden kann. In Demo 52 wird zum Vergleich die geostatistische Vorhersage durch Gradienten-Kriging gegenübergestellt. Sie wurde mit einer angepaßten Kovarianzfunktion unter Benutzung der 5 Stützpunkte und Tangenten an den Wendestellen des Sollprofils abgeleitet, die auch für die BEZIER-Kurve ausgewählt worden sind.
Nicht im Detail berücksichtigt worden sind die Krümmungsradien. Die Krümmung in Demo 52 wird über die GAUSSsche Kovarianzfunktion gesteuert. Aus dieser dadurch reduzierten Informationsmenge erklärt sich die etwas größere Abweichung in der Approximation durch Kriging. Bei der Kombination Stützpunkt-Gradient reicht es aus, wenn nur an jeder zweiten Wendestelle gemessen wird.
Wie in den nachfolgenden Kapiteln 6 und 7 dargestellt werden wird, bilden sogenannte kernfunktionsbasierte Vorhersagen einen sehr allgemeinen Rahmen, in den sich sowohl die geostatistischen als auch weitere noch zu behandelnde Verfahren einordnen lassen. Dazu gehört auch die Multiquadratische Methode, auf die hier näher eingegangen werden soll. Sie ist als algebraische Methode einzustufen und wird von vielen Autoren für die Vorhersage empfohlen.
Die Unterschiede zwischen Kriging und Mulitquadratischer Methode (MQM) bestehen in den unterschiedlichen Kernfunktionen. Beim Kriging benutzt man als Kernfunktion die Kovarianzfunktion oder ihr Spiegelbild, das Variogramm (Bild 14). Für ein GAUSSsches Variogramm wird beispielsweise beim Auftreten einer Störgröße folgende Beziehung benutzt:
 ( 4.4 )
( 4.4 )
Bild 17 zeigt den Verlauf dieses Variogramms für die Parameter
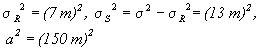 ( 4.5 )
( 4.5 )
Als Kernfunktion der MQM wird die Funktion
 ( 4.6 )
( 4.6 )
benutzt. Das Argument s ist der Abstand zwischen den Punkten des Raumbereiches. Mit g wird eine sogenannte Glättungsgröße eingeführt, die die Krümmung und die Anpassung bei der MQM steuert.
Für g = 50 m wird in Bild 17 neben dem Variogramm der Verlauf der Kernfunktion (4.6) dargestellt. Die Ähnlichkeit der beiden Kurven ist auffallend. Sie resultiert daraus, daß hier, auf g abgestimmt, die Variogrammparameter (4.5) ausgewählt worden sind. In der Praxis ist es umgekehrt. Das Variogramm liegt vor. Es wird aus den Meßwerten abgeleitet. An das Variogramm sollte eine Kernfunktion (4.6) möglichst gut angepaßt werden, was über die Variation von g erreicht werden kann. Bei guter Anpassung ergeben sich erst mit wachsendem s Unterschiede, die man durch eine entsprechende Beschränkung des Einwirkungsbereiches bei der Vorhersage ausschließen könnte. Wenn man eine Kernfunktion auswählen kann, die dem an die Daten angepaßten Variogramm ähnlich ist, dann kann man auf dem Wege der kernfunktionsbasierten Vorhersage, hier z. B. durch die Multiquadratische Methode, so gute Vorhersagen erwarten wie beim Kriging, was an den folgenden Demos noch gezeigt werden soll.
In Demo 53 wird durch die stark ausgezogene Kurve gezeigt, wie die Vorhersage mit der Multiquadratischen Methode ausfällt, wenn die in Bild 17 dargestellte Kernfunktion mit g = 50 m benutzt wird. Um die Effekte besser diskutieren zu können, wird wieder mit einem für die Vorhersage des Sollprofils unzureichenden Datensatz gearbeitet, der lediglich 4 Stützwerte enthält. Man sieht, daß die Multiquadratische Methode zu meßpunkttreuen Vorhersagen führt. Bei g größer Null erhält man glatte Kurven (fließende Übergänge) und bei g = 0 geradlinige Verbindungen zwischen den Stützwerten, wie in Demo 54 durch die mittelstark ausgezogene Linie gezeigt wird. Eine vorhergesagte Fläche entspricht in diesem Fall den kantigen Formen eines meßpunkttreuen Polyeders, dessen Spur in Vertikalschnitten, wie hier, als Polygon abgebildet wird. Bild 17 zeigt auch den Verlauf von (4.6) für g = 0.
In Bild 17 wurden die Scheitelpunkte beider Kurven über die Einführung einer fingierten Störgrößenstreuung mit
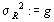 ( 4.7 )
( 4.7 )
zur Koinzidenz gebracht, weil man dadurch die gute Übereinstimmung beider Kurven noch besser erkennen kann. Nimmt man nun an, daß tatsächlich so eine Störgrößenstreuung vorliegen würde, dann müßte man die Meßpunkttreue bei der Vorhersage verlassen und diese Störung eliminieren, so wie es beispielsweise der Übergang von Demo 2 zu Demo 6 zeigt, wenn man sich in Demo 6 die Spitzen an den Meßpunkten wegdenkt.
In Anlehnung an Kriging könnte man nun auch die MQM so gestalten, daß die Filterung eintritt. Zu diesem Zweck sind die nach (4.6) berechneten Elemente der Hauptdiagonale der Matrix der Kernfunktionen um entsprechende Beträge D
i zu senken, die den Störgrößenstreuungen von zi entsprechen. In Demo 53 wird durch die unterbrochene Linie die MQM mit Filterung (D
i = g) gezeigt. In Demo 54 und 55 wird gezeigt, daß man auch in diesem Fall die Meßpunkttreue erzwingen kann, und zwar dann, wenn diese Absenkung um D
i bei s = 0 auch im Kernfunktionsvektor vorgenommen wird, was natürlich unsinnig ist. Eine Absenkung um g bei s = 0 bedeutet, daß die entsprechenden Elemente den Wert null annehmen (Demos).
Nun soll diskutiert werden, daß bei der MQM meßpunkttreu vorhergesagt wird (vergleiche Demo 53, stark ausgezogene Kurve), auch wenn das Bild der Kernfunktion dem eines Variogramms mit Störgrößenanteil zu entsprechen scheint (vergleiche Bild 17). So gesehen, müßte auch unter Verwendung eines an die Kernfunktion angepaßten Variogramms
 ( 4.8 )
( 4.8 )
geostatistisch meßpunkttreu, wie in Demo 53 durch die stark ausgezogene Kurve gezeigt, vorhergesagt werden können. Belegt man die Elemente der Variogrammatrix und des Variogrammvektors nach (4.8), dann ist das tatsächlich möglich. Im Unterschied zu (4.4) wird dabei in (4.8) der Fall s = 0 nicht anders behandelt. Betrachtet man die so gebildeten Kriging-Gleichungssysteme, bei denen alle Elemente nach (4.8) den Zuschlag 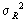 erhalten haben, dann stellt man fest, daß dieser ohne Probleme eliminiert werden kann. Es wird so vorhergesagt, als wäre nur das Variogramm des Signalanteils vorhanden. In (4.8) kann
erhalten haben, dann stellt man fest, daß dieser ohne Probleme eliminiert werden kann. Es wird so vorhergesagt, als wäre nur das Variogramm des Signalanteils vorhanden. In (4.8) kann 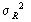 als ein auf die Vorhersage einflußloser Operator angesehen werden, dessen Werte beliebig wählbar sind und der hier nur dazu benutzt werden soll, die Koinzidenz der Scheitelpunkte nach (4.7) herbeizuführen, um Kernfunktion und Variogramm besser miteinander vergleichen zu können.
Die Überlegungen haben gezeigt, daß über die Glättungsgröße g lediglich der Krümmungsverlauf der hyperbolischen Kernfunktionen der MQM gesteuert wird, so daß sie damit an ein auf die Daten abgestimmtes Variogramm angepaßt werden können. Unabhänig von g muß außerdem D
i bestimmt werden, wenn Störgrößen auftreten und diese bei der MQM-Vorhersage eliminiert werden sollen. Forschungsarbeiten zur Auswahl zweckmäßiger Kernfunktionen und zur Festlegung ihrer Parameter sind noch erforderlich.
In Kapitel 7 soll gezeigt werden, wie kernfunktionsbasierte Vorhersagen erweitert werden müssen, damit man auch Gradienten bei der Vorhersage berücksichtigen kann. Die für die Lösung dieser Aufgabe von uns entwickelten Verfahren werden mit der Software SAFARI zur allgemeinen Nutzung über das Internet bereitgestellt. Die folgenden Demos sollen zeigen, wie die Vorhersagen auf der Basis von Gradienten aussehen, wenn mit einem Datensatz von 10 Gradienten gearbeitet wird, der das Sollprofil wieder an allen Wendepunkten, also vollständig erfaßt. Für die absolute Orientierung werden in den Demos 56 bis 60 und 64 jeweils 2 Stützwerte benutzt. In den Demos 61 bis 63 wird nur 1 Stützwert verwendet.
Demo 56 zeigt den Vergleich zwischen MQM, Kriging und Sollwerten. In Demo 57 wird demonstriert, welchen Einfluß eine Filterung D
i = g auf eine gradientengestützte MQM hat. In Demo 58 ist eine Vohersage mit der inversen MQM (siehe Kapitel 7) zu sehen. Man erkennt, daß dabei g = 50 m kein günstiger Wert für die Glättungsgröße ist. Dagegen erhält man mit g = 100 bzw. 90 m bessere Ergebnisse, wie die Demos 59 und 60 zeigen. In den Demos 56, 58 bis 60 und 62 wird die Vorhersage durch Gradienten-Kriging jeweils zum Vergleich mit angegeben. In dem Demos 61 bis 63 wird nur 1 Stützwert benutzt. Gegenübergestellt werden in diesen Demos MQM- und inverse MQM-Vorhersagen mit unterschiedlicher Glättungsgröße g. Schließlich wird in Demo 64 die Vorhersage mit der Sinc-Funktion als Kernfunktion gezeigt (siehe Kapitel 7).
Am Ende dieses Kapitels soll in Demos gezeigt werden, welchen Einfluß die Abstände zwischen den Meßstellen auf die Vorhersageergebnisse haben. Dazu werden die in den Demos 65 und 66 dargestellten Datensätze benutzt. Demo 65 zeigt, wie ein Datensatz von 10 Stützwerten auf 20 und schließlich 40 Stützwerte verdichtet worden ist. Um die Datensätze besser zeigen zu können, werden sie höhenversetzt (um 0, 10 und 20 m) dargestellt. Die Datensätze für Gradienten umfassen 10, 20 und 40 Gradienten mit 2 bzw. 3 Stützwerten. Sie sind (um 0, 10, 20 und 30 m) höhenversetzt in Demo 66 dargestellt worden.
In den Demos 67 und 68 wird für die MQM gezeigt, daß bei einer konstanten Glättungsgröße g = 50 m unabhänig von Stützpunktabstand gute Vorhersageergebnisse erzielt werden können. Auch eine Änderung des Abstandes zwischen den Gradienten hat bei der MQM keinen Einfluß, wie die Demos 69 bis 71 zeigen. Der unstetige Verlauf der MQM mit 40 Gradienten und 2 Stützwerten in Demo 70 kommt dadurch zustande, daß mit einer Beschränkung auf 16 Gradienten im Einwirkungsbereich gearbeitet worden ist, so daß das Prinzip der vollständigen Erfassung in der Profilmitte verletzt wird. Ein zusätzlicher Stützwert in der Mitte behebt diesen Effekt, wie man in Demo 71 sieht.
Untersuchungen zum Einfluß des Stützpunktabstandes auf die Vorhersagen, hier anhand von Demos, werden deshalb gezeigt, weil die Glättungsgröße g nach der Literatur allein aus dem Stützpunktabstand ermittelt werden soll! Wegen der im Rahmen dieser Forschung festgestellten Parallelen zwischen Kriging und MQM, wird in dieser Arbeit diskutiert, daß auch eine Anpassung der Kernfunktionen an das Variogramm sinnvoll sein kann.
Das Variogramm wird aus den Stützwerten abgeleitet und spiegelt das dem zu untersuchenden Merkmal innewohnende Schwingungsverhalten wider (Spektraldarstellung der Kovarianzfunktion). Man muß den Erkundungsabstand so wählen, daß alle relevanten Schwingungen erfaßt werden. Eine dichtere Erkundung bringt dann keine neue Information für die Vorhersage, wie unsere Demos zeigen. Sie erhöht die Kosten und führt zu numerischen Problemen bei der Auswertung, was im folgenden gezeigt werden soll. Bei einem optimal auf das relevante Schwingungverhalten des Merkmals abgestimmten Erkundungsabstand ist der Vorschlag aus der Literatur, g aus dem Stützpunktabstand zu ermitteln, sinnvoll.
In den nun folgenden Demos 72 bis 78 soll mit den Datensätzen ausDemo 65 und 66 auch für die geostatistische Vorhersage mit einer GAUSSschen Kovarianzfunktion gezeigt werden, wie sich eine zu hohe Beprobungsdichte auswirken kann. In allen Demos werden die angepaßten Modellparameter benutzt.
Die Demos 72 und 73 zeigen, daß die Variation des Stützpunktabstandes keinen Einfluß auf das Vorhersageergebnis hat, wenn die Anzahl der Stützpunkte im EWB auf 30 begrenzt wird. In den Demos 74 bis 76 wurde mit Gradienten-Kriging gearbeitet. Auch hier stellt man fest, daß die Verringerung des Gradientenabstandes problemlos bewältigt worden ist. In Demo 76 wird ein Ergebnis präsentiert, das man erhält, wenn stets mit allen 40 Gradienten im EWB vorhergesagt wird. In Demo 74 wurde eine Beschränkung auf 16 Gradienten im EWB vorgenommen, was zu den kleinen Unregelmäßigkeiten in der Mitte des Profils führt. Sie verschwinden, wenn globales Kriging durchgeführt wird, wie Demo 75 zeigt.
In den Demos 77 und 78 werden die numerischen Effekte demonstriert, die bei GAUSSchen Kovarianzfunktionen auftreten können, wenn zu viele dicht beieinanderliegende Stützwerte zur Vorhersage herangezogen werden. Man kann solche Effekte vermeiden, wenn zur Vorhersage weniger Stützwerte herangezogen werden, was über eine Verringerung des EWB zu erreichen ist. Hervorgehoben werden soll, daß die numerischen Probleme nicht sofort zu erkennen sind. Wie die Demos 77 und 78 zeigen, erhält man mit kontinuierlich wachsender Größe a = 1/a
auch kontinuierlich wachsende Abweichungen. Die Kurvenverläufe sind fließend und erwecken den Anschein, daß sie richtig seien. Erst bei näherer Betrachtung erkennt man die Abweichungen. Die Meßpunkttreue geht verloren. Ob dieser Effekt eintritt, sollte zuerst geprüft werden.
Bemerkenswert ist, daß die numerischen Probleme GAUSSscher Kovarianzfunktionen erst bei einem geringeren Meßstellenabstand eintreten, wenn auf der Basis von Gradienten und nicht auf der Basis von Stützwerten vorhergesagt wird (vergleiche Demo 76 und 77), obwohl die Kriging-Gleichungssysteme mehr als doppelt so groß sind. Der Grund dafür ist, daß GAUSSsche Kovarianzfunktionen nicht so stark fallen wie ihre Ableitungen.
Bemerkt werden soll schließlich, daß man auch über eine Additionskonstante regularisierend auf die Vorhersagen einwirken kann. In diesem Fall nimmt man eine Glättung und den Verlust der Meßpunkttreue in Kauf.
als ein auf die Vorhersage einflußloser Operator angesehen werden, dessen Werte beliebig wählbar sind und der hier nur dazu benutzt werden soll, die Koinzidenz der Scheitelpunkte nach (4.7) herbeizuführen, um Kernfunktion und Variogramm besser miteinander vergleichen zu können.
Die Überlegungen haben gezeigt, daß über die Glättungsgröße g lediglich der Krümmungsverlauf der hyperbolischen Kernfunktionen der MQM gesteuert wird, so daß sie damit an ein auf die Daten abgestimmtes Variogramm angepaßt werden können. Unabhänig von g muß außerdem D
i bestimmt werden, wenn Störgrößen auftreten und diese bei der MQM-Vorhersage eliminiert werden sollen. Forschungsarbeiten zur Auswahl zweckmäßiger Kernfunktionen und zur Festlegung ihrer Parameter sind noch erforderlich.
In Kapitel 7 soll gezeigt werden, wie kernfunktionsbasierte Vorhersagen erweitert werden müssen, damit man auch Gradienten bei der Vorhersage berücksichtigen kann. Die für die Lösung dieser Aufgabe von uns entwickelten Verfahren werden mit der Software SAFARI zur allgemeinen Nutzung über das Internet bereitgestellt. Die folgenden Demos sollen zeigen, wie die Vorhersagen auf der Basis von Gradienten aussehen, wenn mit einem Datensatz von 10 Gradienten gearbeitet wird, der das Sollprofil wieder an allen Wendepunkten, also vollständig erfaßt. Für die absolute Orientierung werden in den Demos 56 bis 60 und 64 jeweils 2 Stützwerte benutzt. In den Demos 61 bis 63 wird nur 1 Stützwert verwendet.
Demo 56 zeigt den Vergleich zwischen MQM, Kriging und Sollwerten. In Demo 57 wird demonstriert, welchen Einfluß eine Filterung D
i = g auf eine gradientengestützte MQM hat. In Demo 58 ist eine Vohersage mit der inversen MQM (siehe Kapitel 7) zu sehen. Man erkennt, daß dabei g = 50 m kein günstiger Wert für die Glättungsgröße ist. Dagegen erhält man mit g = 100 bzw. 90 m bessere Ergebnisse, wie die Demos 59 und 60 zeigen. In den Demos 56, 58 bis 60 und 62 wird die Vorhersage durch Gradienten-Kriging jeweils zum Vergleich mit angegeben. In dem Demos 61 bis 63 wird nur 1 Stützwert benutzt. Gegenübergestellt werden in diesen Demos MQM- und inverse MQM-Vorhersagen mit unterschiedlicher Glättungsgröße g. Schließlich wird in Demo 64 die Vorhersage mit der Sinc-Funktion als Kernfunktion gezeigt (siehe Kapitel 7).
Am Ende dieses Kapitels soll in Demos gezeigt werden, welchen Einfluß die Abstände zwischen den Meßstellen auf die Vorhersageergebnisse haben. Dazu werden die in den Demos 65 und 66 dargestellten Datensätze benutzt. Demo 65 zeigt, wie ein Datensatz von 10 Stützwerten auf 20 und schließlich 40 Stützwerte verdichtet worden ist. Um die Datensätze besser zeigen zu können, werden sie höhenversetzt (um 0, 10 und 20 m) dargestellt. Die Datensätze für Gradienten umfassen 10, 20 und 40 Gradienten mit 2 bzw. 3 Stützwerten. Sie sind (um 0, 10, 20 und 30 m) höhenversetzt in Demo 66 dargestellt worden.
In den Demos 67 und 68 wird für die MQM gezeigt, daß bei einer konstanten Glättungsgröße g = 50 m unabhänig von Stützpunktabstand gute Vorhersageergebnisse erzielt werden können. Auch eine Änderung des Abstandes zwischen den Gradienten hat bei der MQM keinen Einfluß, wie die Demos 69 bis 71 zeigen. Der unstetige Verlauf der MQM mit 40 Gradienten und 2 Stützwerten in Demo 70 kommt dadurch zustande, daß mit einer Beschränkung auf 16 Gradienten im Einwirkungsbereich gearbeitet worden ist, so daß das Prinzip der vollständigen Erfassung in der Profilmitte verletzt wird. Ein zusätzlicher Stützwert in der Mitte behebt diesen Effekt, wie man in Demo 71 sieht.
Untersuchungen zum Einfluß des Stützpunktabstandes auf die Vorhersagen, hier anhand von Demos, werden deshalb gezeigt, weil die Glättungsgröße g nach der Literatur allein aus dem Stützpunktabstand ermittelt werden soll! Wegen der im Rahmen dieser Forschung festgestellten Parallelen zwischen Kriging und MQM, wird in dieser Arbeit diskutiert, daß auch eine Anpassung der Kernfunktionen an das Variogramm sinnvoll sein kann.
Das Variogramm wird aus den Stützwerten abgeleitet und spiegelt das dem zu untersuchenden Merkmal innewohnende Schwingungsverhalten wider (Spektraldarstellung der Kovarianzfunktion). Man muß den Erkundungsabstand so wählen, daß alle relevanten Schwingungen erfaßt werden. Eine dichtere Erkundung bringt dann keine neue Information für die Vorhersage, wie unsere Demos zeigen. Sie erhöht die Kosten und führt zu numerischen Problemen bei der Auswertung, was im folgenden gezeigt werden soll. Bei einem optimal auf das relevante Schwingungverhalten des Merkmals abgestimmten Erkundungsabstand ist der Vorschlag aus der Literatur, g aus dem Stützpunktabstand zu ermitteln, sinnvoll.
In den nun folgenden Demos 72 bis 78 soll mit den Datensätzen ausDemo 65 und 66 auch für die geostatistische Vorhersage mit einer GAUSSschen Kovarianzfunktion gezeigt werden, wie sich eine zu hohe Beprobungsdichte auswirken kann. In allen Demos werden die angepaßten Modellparameter benutzt.
Die Demos 72 und 73 zeigen, daß die Variation des Stützpunktabstandes keinen Einfluß auf das Vorhersageergebnis hat, wenn die Anzahl der Stützpunkte im EWB auf 30 begrenzt wird. In den Demos 74 bis 76 wurde mit Gradienten-Kriging gearbeitet. Auch hier stellt man fest, daß die Verringerung des Gradientenabstandes problemlos bewältigt worden ist. In Demo 76 wird ein Ergebnis präsentiert, das man erhält, wenn stets mit allen 40 Gradienten im EWB vorhergesagt wird. In Demo 74 wurde eine Beschränkung auf 16 Gradienten im EWB vorgenommen, was zu den kleinen Unregelmäßigkeiten in der Mitte des Profils führt. Sie verschwinden, wenn globales Kriging durchgeführt wird, wie Demo 75 zeigt.
In den Demos 77 und 78 werden die numerischen Effekte demonstriert, die bei GAUSSchen Kovarianzfunktionen auftreten können, wenn zu viele dicht beieinanderliegende Stützwerte zur Vorhersage herangezogen werden. Man kann solche Effekte vermeiden, wenn zur Vorhersage weniger Stützwerte herangezogen werden, was über eine Verringerung des EWB zu erreichen ist. Hervorgehoben werden soll, daß die numerischen Probleme nicht sofort zu erkennen sind. Wie die Demos 77 und 78 zeigen, erhält man mit kontinuierlich wachsender Größe a = 1/a
auch kontinuierlich wachsende Abweichungen. Die Kurvenverläufe sind fließend und erwecken den Anschein, daß sie richtig seien. Erst bei näherer Betrachtung erkennt man die Abweichungen. Die Meßpunkttreue geht verloren. Ob dieser Effekt eintritt, sollte zuerst geprüft werden.
Bemerkenswert ist, daß die numerischen Probleme GAUSSscher Kovarianzfunktionen erst bei einem geringeren Meßstellenabstand eintreten, wenn auf der Basis von Gradienten und nicht auf der Basis von Stützwerten vorhergesagt wird (vergleiche Demo 76 und 77), obwohl die Kriging-Gleichungssysteme mehr als doppelt so groß sind. Der Grund dafür ist, daß GAUSSsche Kovarianzfunktionen nicht so stark fallen wie ihre Ableitungen.
Bemerkt werden soll schließlich, daß man auch über eine Additionskonstante regularisierend auf die Vorhersagen einwirken kann. In diesem Fall nimmt man eine Glättung und den Verlust der Meßpunkttreue in Kauf.
Andree Röttig
Mon Mar 2 17:42:57 MET 1998
 ( 4.4 )
( 4.4 )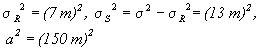 ( 4.5 )
( 4.5 )